mathworld.wolfram.com/LeastSquaresFittingPolynomial.html

Preview meta tags from the mathworld.wolfram.com website.

Linked Hostnames

5

Thumbnail

Search Engine Appearance

Google

https://mathworld.wolfram.com/LeastSquaresFittingPolynomial.html

Least Squares Fitting--Polynomial -- from Wolfram MathWorld

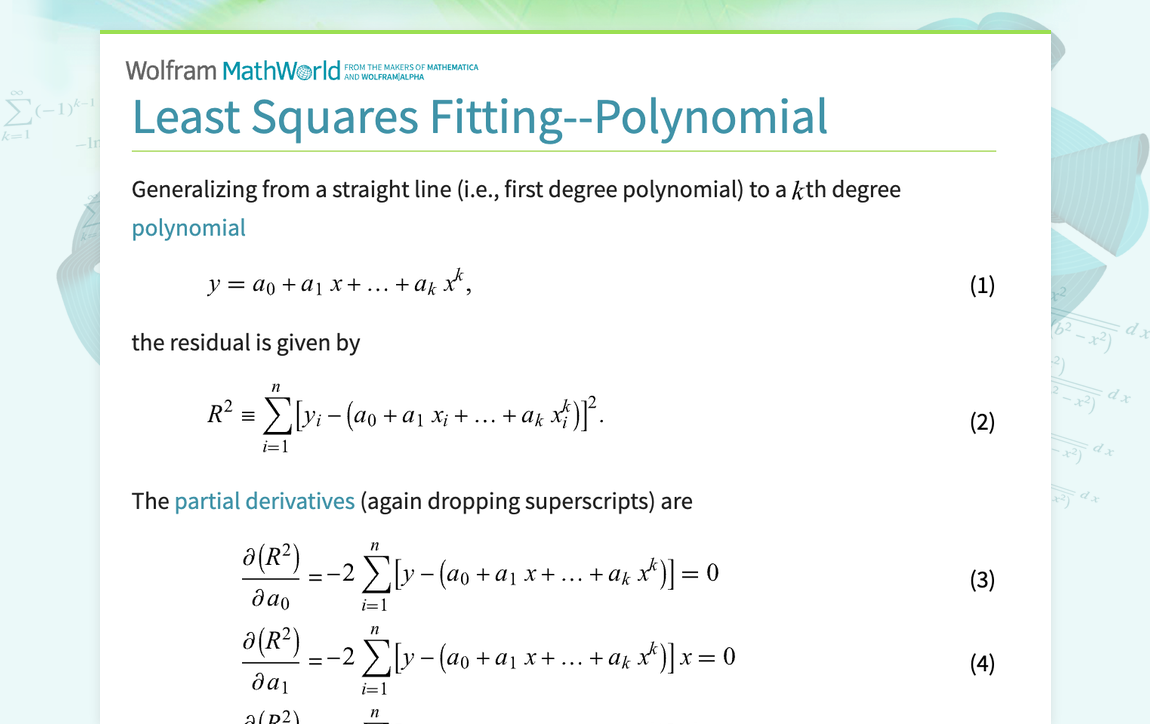
Generalizing from a straight line (i.e., first degree polynomial) to a kth degree polynomial y=a_0+a_1x+...+a_kx^k, (1) the residual is given by R^2=sum_(i=1)^n[y_i-(a_0+a_1x_i+...+a_kx_i^k)]^2. (2) The partial derivatives (again dropping superscripts) are (partial(R^2))/(partiala_0) = -2sum_(i=1)^(n)[y-(a_0+a_1x+...+a_kx^k)]=0 (3) (partial(R^2))/(partiala_1) = -2sum_(i=1)^(n)[y-(a_0+a_1x+...+a_kx^k)]x=0 (4) (partial(R^2))/(partiala_k) =...



Bing

Least Squares Fitting--Polynomial -- from Wolfram MathWorld

https://mathworld.wolfram.com/LeastSquaresFittingPolynomial.html

Generalizing from a straight line (i.e., first degree polynomial) to a kth degree polynomial y=a_0+a_1x+...+a_kx^k, (1) the residual is given by R^2=sum_(i=1)^n[y_i-(a_0+a_1x_i+...+a_kx_i^k)]^2. (2) The partial derivatives (again dropping superscripts) are (partial(R^2))/(partiala_0) = -2sum_(i=1)^(n)[y-(a_0+a_1x+...+a_kx^k)]=0 (3) (partial(R^2))/(partiala_1) = -2sum_(i=1)^(n)[y-(a_0+a_1x+...+a_kx^k)]x=0 (4) (partial(R^2))/(partiala_k) =...



DuckDuckGo

https://mathworld.wolfram.com/LeastSquaresFittingPolynomial.html

Least Squares Fitting--Polynomial -- from Wolfram MathWorld

Generalizing from a straight line (i.e., first degree polynomial) to a kth degree polynomial y=a_0+a_1x+...+a_kx^k, (1) the residual is given by R^2=sum_(i=1)^n[y_i-(a_0+a_1x_i+...+a_kx_i^k)]^2. (2) The partial derivatives (again dropping superscripts) are (partial(R^2))/(partiala_0) = -2sum_(i=1)^(n)[y-(a_0+a_1x+...+a_kx^k)]=0 (3) (partial(R^2))/(partiala_1) = -2sum_(i=1)^(n)[y-(a_0+a_1x+...+a_kx^k)]x=0 (4) (partial(R^2))/(partiala_k) =...

  • General Meta Tags

    21
    • title
      Least Squares Fitting--Polynomial -- from Wolfram MathWorld
    • DC.Title
      Least Squares Fitting--Polynomial
    • DC.Creator
      Weisstein, Eric W.
    • DC.Description
      Generalizing from a straight line (i.e., first degree polynomial) to a kth degree polynomial y=a_0+a_1x+...+a_kx^k, (1) the residual is given by R^2=sum_(i=1)^n[y_i-(a_0+a_1x_i+...+a_kx_i^k)]^2. (2) The partial derivatives (again dropping superscripts) are (partial(R^2))/(partiala_0) = -2sum_(i=1)^(n)[y-(a_0+a_1x+...+a_kx^k)]=0 (3) (partial(R^2))/(partiala_1) = -2sum_(i=1)^(n)[y-(a_0+a_1x+...+a_kx^k)]x=0 (4) (partial(R^2))/(partiala_k) =...
    • description
      Generalizing from a straight line (i.e., first degree polynomial) to a kth degree polynomial y=a_0+a_1x+...+a_kx^k, (1) the residual is given by R^2=sum_(i=1)^n[y_i-(a_0+a_1x_i+...+a_kx_i^k)]^2. (2) The partial derivatives (again dropping superscripts) are (partial(R^2))/(partiala_0) = -2sum_(i=1)^(n)[y-(a_0+a_1x+...+a_kx^k)]=0 (3) (partial(R^2))/(partiala_1) = -2sum_(i=1)^(n)[y-(a_0+a_1x+...+a_kx^k)]x=0 (4) (partial(R^2))/(partiala_k) =...

  • Open Graph Meta Tags

    5
    • og:image
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_LeastSquaresFittingPolynomial.png
    • og:url
      https://mathworld.wolfram.com/LeastSquaresFittingPolynomial.html
    • og:type
      website
    • og:title
      Least Squares Fitting--Polynomial -- from Wolfram MathWorld
    • og:description
      Generalizing from a straight line (i.e., first degree polynomial) to a kth degree polynomial y=a_0+a_1x+...+a_kx^k, (1) the residual is given by R^2=sum_(i=1)^n[y_i-(a_0+a_1x_i+...+a_kx_i^k)]^2. (2) The partial derivatives (again dropping superscripts) are (partial(R^2))/(partiala_0) = -2sum_(i=1)^(n)[y-(a_0+a_1x+...+a_kx^k)]=0 (3) (partial(R^2))/(partiala_1) = -2sum_(i=1)^(n)[y-(a_0+a_1x+...+a_kx^k)]x=0 (4) (partial(R^2))/(partiala_k) =...

  • Twitter Meta Tags

    5
    • twitter:card
      summary_large_image
    • twitter:site
      @WolframResearch
    • twitter:title
      Least Squares Fitting--Polynomial -- from Wolfram MathWorld
    • twitter:description
      Generalizing from a straight line (i.e., first degree polynomial) to a kth degree polynomial y=a_0+a_1x+...+a_kx^k, (1) the residual is given by R^2=sum_(i=1)^n[y_i-(a_0+a_1x_i+...+a_kx_i^k)]^2. (2) The partial derivatives (again dropping superscripts) are (partial(R^2))/(partiala_0) = -2sum_(i=1)^(n)[y-(a_0+a_1x+...+a_kx^k)]=0 (3) (partial(R^2))/(partiala_1) = -2sum_(i=1)^(n)[y-(a_0+a_1x+...+a_kx^k)]x=0 (4) (partial(R^2))/(partiala_k) =...
    • twitter:image:src
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_LeastSquaresFittingPolynomial.png

  • Link Tags

    4
    • canonical
      https://mathworld.wolfram.com/LeastSquaresFittingPolynomial.html
    • preload
      //www.wolframcdn.com/fonts/source-sans-pro/1.0/global.css
    • stylesheet
      /css/styles.css
    • stylesheet
      /common/js/c2c/1.0/WolframC2CGui.css.en

Links

38