
mathworld.wolfram.com/LeastSquaresFitting.html
Preview meta tags from the mathworld.wolfram.com website.
Linked Hostnames
6- 47 links tomathworld.wolfram.com
- 13 links towww.amazon.com
- 4 links towww.wolfram.com
- 4 links towww.wolframalpha.com
- 1 link towolframalpha.com
- 1 link towww.amazon.de
Thumbnail
Search Engine Appearance
Least Squares Fitting -- from Wolfram MathWorld
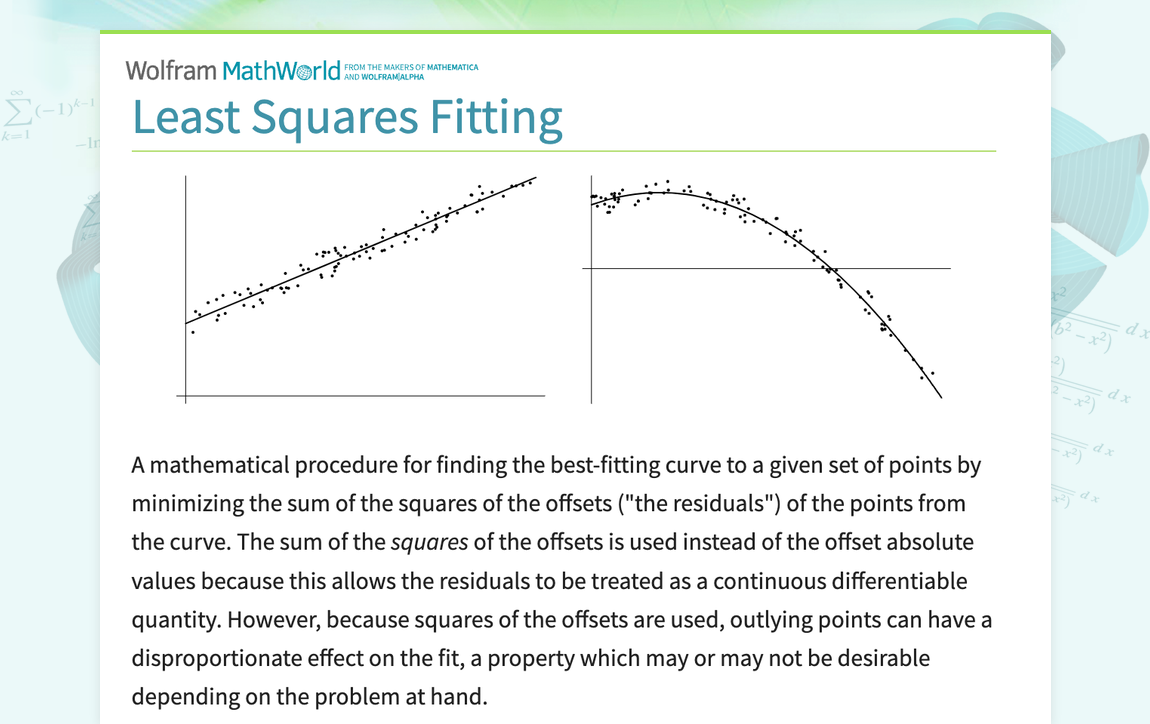
A mathematical procedure for finding the best-fitting curve to a given set of points by minimizing the sum of the squares of the offsets ("the residuals") of the points from the curve. The sum of the squares of the offsets is used instead of the offset absolute values because this allows the residuals to be treated as a continuous differentiable quantity. However, because squares of the offsets are used, outlying points can have a disproportionate effect on the fit, a property...
Bing
Least Squares Fitting -- from Wolfram MathWorld
A mathematical procedure for finding the best-fitting curve to a given set of points by minimizing the sum of the squares of the offsets ("the residuals") of the points from the curve. The sum of the squares of the offsets is used instead of the offset absolute values because this allows the residuals to be treated as a continuous differentiable quantity. However, because squares of the offsets are used, outlying points can have a disproportionate effect on the fit, a property...
DuckDuckGo
Least Squares Fitting -- from Wolfram MathWorld
A mathematical procedure for finding the best-fitting curve to a given set of points by minimizing the sum of the squares of the offsets ("the residuals") of the points from the curve. The sum of the squares of the offsets is used instead of the offset absolute values because this allows the residuals to be treated as a continuous differentiable quantity. However, because squares of the offsets are used, outlying points can have a disproportionate effect on the fit, a property...
General Meta Tags
22- titleLeast Squares Fitting -- from Wolfram MathWorld
- DC.TitleLeast Squares Fitting
- DC.CreatorWeisstein, Eric W.
- DC.DescriptionA mathematical procedure for finding the best-fitting curve to a given set of points by minimizing the sum of the squares of the offsets ("the residuals") of the points from the curve. The sum of the squares of the offsets is used instead of the offset absolute values because this allows the residuals to be treated as a continuous differentiable quantity. However, because squares of the offsets are used, outlying points can have a disproportionate effect on the fit, a property...
- descriptionA mathematical procedure for finding the best-fitting curve to a given set of points by minimizing the sum of the squares of the offsets ("the residuals") of the points from the curve. The sum of the squares of the offsets is used instead of the offset absolute values because this allows the residuals to be treated as a continuous differentiable quantity. However, because squares of the offsets are used, outlying points can have a disproportionate effect on the fit, a property...
Open Graph Meta Tags
5- og:imagehttps://mathworld.wolfram.com/images/socialmedia/share/ogimage_LeastSquaresFitting.png
- og:urlhttps://mathworld.wolfram.com/LeastSquaresFitting.html
- og:typewebsite
- og:titleLeast Squares Fitting -- from Wolfram MathWorld
- og:descriptionA mathematical procedure for finding the best-fitting curve to a given set of points by minimizing the sum of the squares of the offsets ("the residuals") of the points from the curve. The sum of the squares of the offsets is used instead of the offset absolute values because this allows the residuals to be treated as a continuous differentiable quantity. However, because squares of the offsets are used, outlying points can have a disproportionate effect on the fit, a property...
Twitter Meta Tags
5- twitter:cardsummary_large_image
- twitter:site@WolframResearch
- twitter:titleLeast Squares Fitting -- from Wolfram MathWorld
- twitter:descriptionA mathematical procedure for finding the best-fitting curve to a given set of points by minimizing the sum of the squares of the offsets ("the residuals") of the points from the curve. The sum of the squares of the offsets is used instead of the offset absolute values because this allows the residuals to be treated as a continuous differentiable quantity. However, because squares of the offsets are used, outlying points can have a disproportionate effect on the fit, a property...
- twitter:image:srchttps://mathworld.wolfram.com/images/socialmedia/share/ogimage_LeastSquaresFitting.png
Link Tags
4- canonicalhttps://mathworld.wolfram.com/LeastSquaresFitting.html
- preload//www.wolframcdn.com/fonts/source-sans-pro/1.0/global.css
- stylesheet/css/styles.css
- stylesheet/common/js/c2c/1.0/WolframC2CGui.css.en
Links
70- http://www.amazon.com/exec/obidos/ASIN/0062731025/ref=nosim/ericstreasuretro
- http://www.amazon.com/exec/obidos/ASIN/0079112439/ref=nosim/ericstreasuretro
- http://www.amazon.com/exec/obidos/ASIN/0124360610/ref=nosim/ericstreasuretro
- http://www.amazon.com/exec/obidos/ASIN/0387985980/ref=nosim/ericstreasuretro
- http://www.amazon.com/exec/obidos/ASIN/0471319465/ref=nosim/ericstreasuretro