mathworld.wolfram.com/HeartCurve.html

Preview meta tags from the mathworld.wolfram.com website.

Linked Hostnames

5

Thumbnail

Search Engine Appearance

Google

https://mathworld.wolfram.com/HeartCurve.html

Heart Curve -- from Wolfram MathWorld

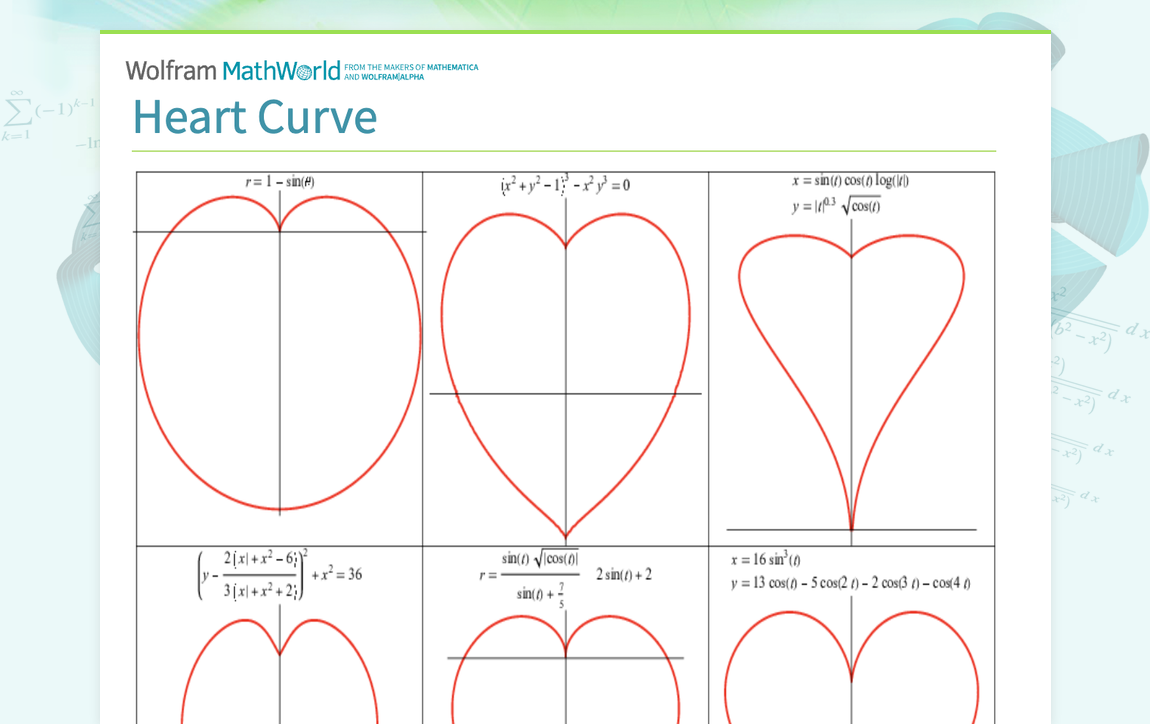
There are a number of mathematical curves that produced heart shapes, some of which are illustrated above. A "zeroth" curve is a rotated cardioid (whose name means "heart-shaped") given by the polar equation r(theta)=1-sintheta. (1) The first heart curve is obtained by taking the y=0 cross section of the heart surface and relabeling the z-coordinates as y, giving the order-6 algebraic equation (x^2+y^2-1)^3-x^2y^3=0. (2) A second heart curve is given by the...



Bing

Heart Curve -- from Wolfram MathWorld

https://mathworld.wolfram.com/HeartCurve.html

There are a number of mathematical curves that produced heart shapes, some of which are illustrated above. A "zeroth" curve is a rotated cardioid (whose name means "heart-shaped") given by the polar equation r(theta)=1-sintheta. (1) The first heart curve is obtained by taking the y=0 cross section of the heart surface and relabeling the z-coordinates as y, giving the order-6 algebraic equation (x^2+y^2-1)^3-x^2y^3=0. (2) A second heart curve is given by the...



DuckDuckGo

https://mathworld.wolfram.com/HeartCurve.html

Heart Curve -- from Wolfram MathWorld

There are a number of mathematical curves that produced heart shapes, some of which are illustrated above. A "zeroth" curve is a rotated cardioid (whose name means "heart-shaped") given by the polar equation r(theta)=1-sintheta. (1) The first heart curve is obtained by taking the y=0 cross section of the heart surface and relabeling the z-coordinates as y, giving the order-6 algebraic equation (x^2+y^2-1)^3-x^2y^3=0. (2) A second heart curve is given by the...

  • General Meta Tags

    34
    • title
      Heart Curve -- from Wolfram MathWorld
    • DC.Title
      Heart Curve
    • DC.Creator
      Weisstein, Eric W.
    • DC.Description
      There are a number of mathematical curves that produced heart shapes, some of which are illustrated above. A "zeroth" curve is a rotated cardioid (whose name means "heart-shaped") given by the polar equation r(theta)=1-sintheta. (1) The first heart curve is obtained by taking the y=0 cross section of the heart surface and relabeling the z-coordinates as y, giving the order-6 algebraic equation (x^2+y^2-1)^3-x^2y^3=0. (2) A second heart curve is given by the...
    • description
      There are a number of mathematical curves that produced heart shapes, some of which are illustrated above. A "zeroth" curve is a rotated cardioid (whose name means "heart-shaped") given by the polar equation r(theta)=1-sintheta. (1) The first heart curve is obtained by taking the y=0 cross section of the heart surface and relabeling the z-coordinates as y, giving the order-6 algebraic equation (x^2+y^2-1)^3-x^2y^3=0. (2) A second heart curve is given by the...

  • Open Graph Meta Tags

    5
    • og:image
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_HeartCurve.png
    • og:url
      https://mathworld.wolfram.com/HeartCurve.html
    • og:type
      website
    • og:title
      Heart Curve -- from Wolfram MathWorld
    • og:description
      There are a number of mathematical curves that produced heart shapes, some of which are illustrated above. A "zeroth" curve is a rotated cardioid (whose name means "heart-shaped") given by the polar equation r(theta)=1-sintheta. (1) The first heart curve is obtained by taking the y=0 cross section of the heart surface and relabeling the z-coordinates as y, giving the order-6 algebraic equation (x^2+y^2-1)^3-x^2y^3=0. (2) A second heart curve is given by the...

  • Twitter Meta Tags

    5
    • twitter:card
      summary_large_image
    • twitter:site
      @WolframResearch
    • twitter:title
      Heart Curve -- from Wolfram MathWorld
    • twitter:description
      There are a number of mathematical curves that produced heart shapes, some of which are illustrated above. A "zeroth" curve is a rotated cardioid (whose name means "heart-shaped") given by the polar equation r(theta)=1-sintheta. (1) The first heart curve is obtained by taking the y=0 cross section of the heart surface and relabeling the z-coordinates as y, giving the order-6 algebraic equation (x^2+y^2-1)^3-x^2y^3=0. (2) A second heart curve is given by the...
    • twitter:image:src
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_HeartCurve.png

  • Link Tags

    4
    • canonical
      https://mathworld.wolfram.com/HeartCurve.html
    • preload
      //www.wolframcdn.com/fonts/source-sans-pro/1.0/global.css
    • stylesheet
      /css/styles.css
    • stylesheet
      /common/js/c2c/1.0/WolframC2CGui.css.en

Links

54