mathworld.wolfram.com/BonneProjection.html

Preview meta tags from the mathworld.wolfram.com website.

Linked Hostnames

6

Thumbnail

Search Engine Appearance

Google

https://mathworld.wolfram.com/BonneProjection.html

Bonne Projection -- from Wolfram MathWorld

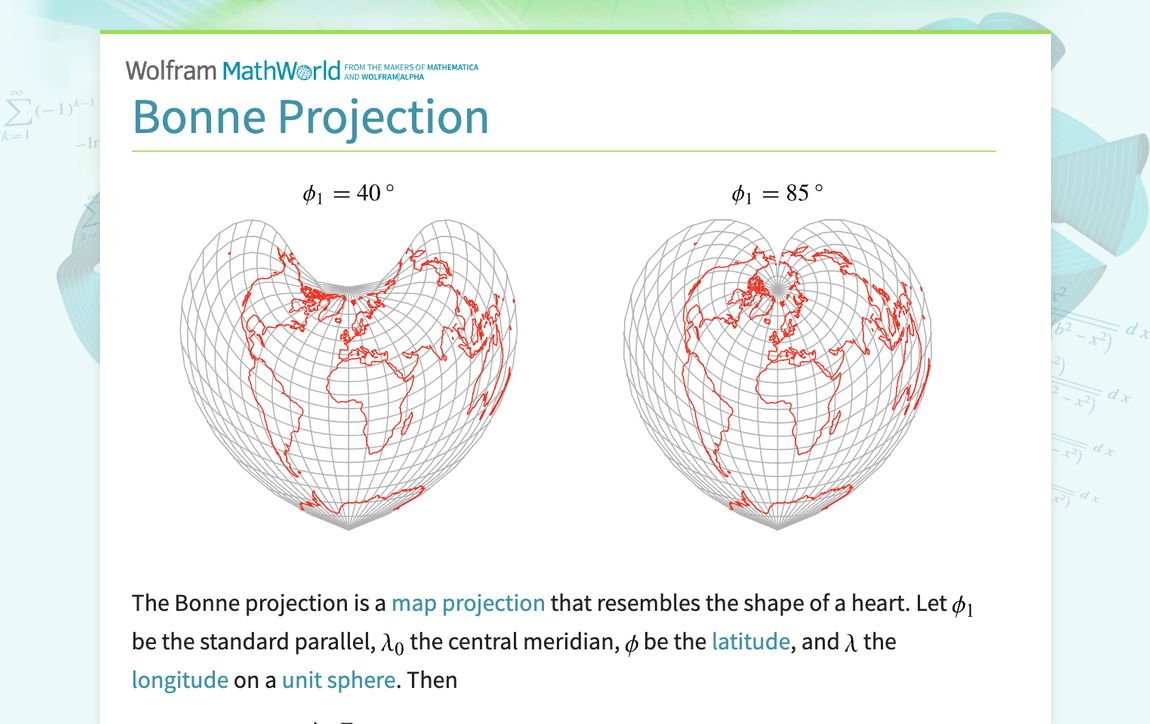
The Bonne projection is a map projection that resembles the shape of a heart. Let phi_1 be the standard parallel, lambda_0 the central meridian, phi be the latitude, and lambda the longitude on a unit sphere. Then x = rhosinE (1) y = cotphi_1-rhocosE, (2) where rho = cotphi_1+phi_1-phi (3) E = ((lambda-lambda_0)cosphi)/rho. (4) The illustrations above show Bonne projections for two different standard parallels. The inverse formulas are phi = cotphi_1+phi_1-rho (5) lambda =...



Bing

Bonne Projection -- from Wolfram MathWorld

https://mathworld.wolfram.com/BonneProjection.html

The Bonne projection is a map projection that resembles the shape of a heart. Let phi_1 be the standard parallel, lambda_0 the central meridian, phi be the latitude, and lambda the longitude on a unit sphere. Then x = rhosinE (1) y = cotphi_1-rhocosE, (2) where rho = cotphi_1+phi_1-phi (3) E = ((lambda-lambda_0)cosphi)/rho. (4) The illustrations above show Bonne projections for two different standard parallels. The inverse formulas are phi = cotphi_1+phi_1-rho (5) lambda =...



DuckDuckGo

https://mathworld.wolfram.com/BonneProjection.html

Bonne Projection -- from Wolfram MathWorld

The Bonne projection is a map projection that resembles the shape of a heart. Let phi_1 be the standard parallel, lambda_0 the central meridian, phi be the latitude, and lambda the longitude on a unit sphere. Then x = rhosinE (1) y = cotphi_1-rhocosE, (2) where rho = cotphi_1+phi_1-phi (3) E = ((lambda-lambda_0)cosphi)/rho. (4) The illustrations above show Bonne projections for two different standard parallels. The inverse formulas are phi = cotphi_1+phi_1-rho (5) lambda =...

  • General Meta Tags

    18
    • title
      Bonne Projection -- from Wolfram MathWorld
    • DC.Title
      Bonne Projection
    • DC.Creator
      Weisstein, Eric W.
    • DC.Description
      The Bonne projection is a map projection that resembles the shape of a heart. Let phi_1 be the standard parallel, lambda_0 the central meridian, phi be the latitude, and lambda the longitude on a unit sphere. Then x = rhosinE (1) y = cotphi_1-rhocosE, (2) where rho = cotphi_1+phi_1-phi (3) E = ((lambda-lambda_0)cosphi)/rho. (4) The illustrations above show Bonne projections for two different standard parallels. The inverse formulas are phi = cotphi_1+phi_1-rho (5) lambda =...
    • description
      The Bonne projection is a map projection that resembles the shape of a heart. Let phi_1 be the standard parallel, lambda_0 the central meridian, phi be the latitude, and lambda the longitude on a unit sphere. Then x = rhosinE (1) y = cotphi_1-rhocosE, (2) where rho = cotphi_1+phi_1-phi (3) E = ((lambda-lambda_0)cosphi)/rho. (4) The illustrations above show Bonne projections for two different standard parallels. The inverse formulas are phi = cotphi_1+phi_1-rho (5) lambda =...

  • Open Graph Meta Tags

    5
    • og:image
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_BonneProjection.png
    • og:url
      https://mathworld.wolfram.com/BonneProjection.html
    • og:type
      website
    • og:title
      Bonne Projection -- from Wolfram MathWorld
    • og:description
      The Bonne projection is a map projection that resembles the shape of a heart. Let phi_1 be the standard parallel, lambda_0 the central meridian, phi be the latitude, and lambda the longitude on a unit sphere. Then x = rhosinE (1) y = cotphi_1-rhocosE, (2) where rho = cotphi_1+phi_1-phi (3) E = ((lambda-lambda_0)cosphi)/rho. (4) The illustrations above show Bonne projections for two different standard parallels. The inverse formulas are phi = cotphi_1+phi_1-rho (5) lambda =...

  • Twitter Meta Tags

    5
    • twitter:card
      summary_large_image
    • twitter:site
      @WolframResearch
    • twitter:title
      Bonne Projection -- from Wolfram MathWorld
    • twitter:description
      The Bonne projection is a map projection that resembles the shape of a heart. Let phi_1 be the standard parallel, lambda_0 the central meridian, phi be the latitude, and lambda the longitude on a unit sphere. Then x = rhosinE (1) y = cotphi_1-rhocosE, (2) where rho = cotphi_1+phi_1-phi (3) E = ((lambda-lambda_0)cosphi)/rho. (4) The illustrations above show Bonne projections for two different standard parallels. The inverse formulas are phi = cotphi_1+phi_1-rho (5) lambda =...
    • twitter:image:src
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_BonneProjection.png

  • Link Tags

    4
    • canonical
      https://mathworld.wolfram.com/BonneProjection.html
    • preload
      //www.wolframcdn.com/fonts/source-sans-pro/1.0/global.css
    • stylesheet
      /css/styles.css
    • stylesheet
      /common/js/c2c/1.0/WolframC2CGui.css.en

Links

41