mathworld.wolfram.com/ImpossibleFork.html

Preview meta tags from the mathworld.wolfram.com website.

Linked Hostnames

6

Thumbnail

Search Engine Appearance

Google

https://mathworld.wolfram.com/ImpossibleFork.html

Impossible Fork -- from Wolfram MathWorld

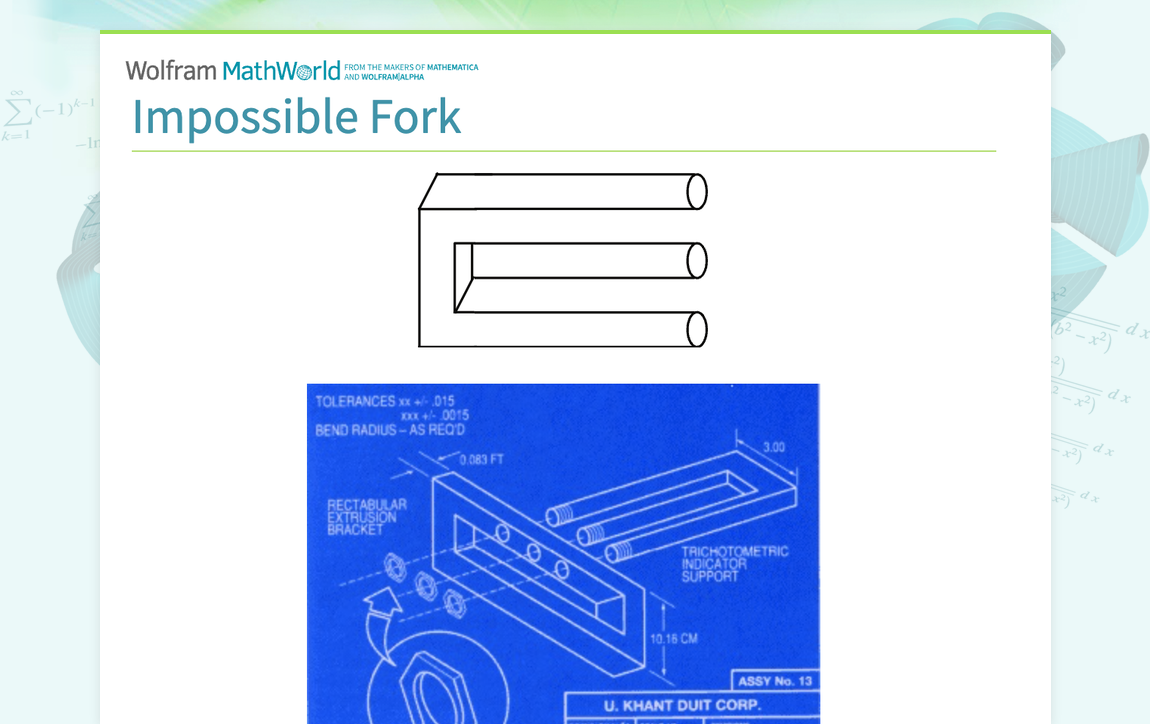
The impossible fork (Seckel 2002, p. 151), also known as the devil's pitchfork (Singmaster), blivet, or poiuyt, is a classic impossible figure originally due to Schuster (1964). While each prong of the fork (or, in the original work, "clevis") appears normal, attempting to determine their manner of attachment shows that something is seriously out of whack. The second figure above shows three impossible figures: the ambihelical hexnut in the lower left-hand corner, tribox in the...



Bing

Impossible Fork -- from Wolfram MathWorld

https://mathworld.wolfram.com/ImpossibleFork.html

The impossible fork (Seckel 2002, p. 151), also known as the devil's pitchfork (Singmaster), blivet, or poiuyt, is a classic impossible figure originally due to Schuster (1964). While each prong of the fork (or, in the original work, "clevis") appears normal, attempting to determine their manner of attachment shows that something is seriously out of whack. The second figure above shows three impossible figures: the ambihelical hexnut in the lower left-hand corner, tribox in the...



DuckDuckGo

https://mathworld.wolfram.com/ImpossibleFork.html

Impossible Fork -- from Wolfram MathWorld

The impossible fork (Seckel 2002, p. 151), also known as the devil's pitchfork (Singmaster), blivet, or poiuyt, is a classic impossible figure originally due to Schuster (1964). While each prong of the fork (or, in the original work, "clevis") appears normal, attempting to determine their manner of attachment shows that something is seriously out of whack. The second figure above shows three impossible figures: the ambihelical hexnut in the lower left-hand corner, tribox in the...

  • General Meta Tags

    22
    • title
      Impossible Fork -- from Wolfram MathWorld
    • DC.Title
      Impossible Fork
    • DC.Creator
      Weisstein, Eric W.
    • DC.Description
      The impossible fork (Seckel 2002, p. 151), also known as the devil's pitchfork (Singmaster), blivet, or poiuyt, is a classic impossible figure originally due to Schuster (1964). While each prong of the fork (or, in the original work, "clevis") appears normal, attempting to determine their manner of attachment shows that something is seriously out of whack. The second figure above shows three impossible figures: the ambihelical hexnut in the lower left-hand corner, tribox in the...
    • description
      The impossible fork (Seckel 2002, p. 151), also known as the devil's pitchfork (Singmaster), blivet, or poiuyt, is a classic impossible figure originally due to Schuster (1964). While each prong of the fork (or, in the original work, "clevis") appears normal, attempting to determine their manner of attachment shows that something is seriously out of whack. The second figure above shows three impossible figures: the ambihelical hexnut in the lower left-hand corner, tribox in the...

  • Open Graph Meta Tags

    5
    • og:image
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_ImpossibleFork.png
    • og:url
      https://mathworld.wolfram.com/ImpossibleFork.html
    • og:type
      website
    • og:title
      Impossible Fork -- from Wolfram MathWorld
    • og:description
      The impossible fork (Seckel 2002, p. 151), also known as the devil's pitchfork (Singmaster), blivet, or poiuyt, is a classic impossible figure originally due to Schuster (1964). While each prong of the fork (or, in the original work, "clevis") appears normal, attempting to determine their manner of attachment shows that something is seriously out of whack. The second figure above shows three impossible figures: the ambihelical hexnut in the lower left-hand corner, tribox in the...

  • Twitter Meta Tags

    5
    • twitter:card
      summary_large_image
    • twitter:site
      @WolframResearch
    • twitter:title
      Impossible Fork -- from Wolfram MathWorld
    • twitter:description
      The impossible fork (Seckel 2002, p. 151), also known as the devil's pitchfork (Singmaster), blivet, or poiuyt, is a classic impossible figure originally due to Schuster (1964). While each prong of the fork (or, in the original work, "clevis") appears normal, attempting to determine their manner of attachment shows that something is seriously out of whack. The second figure above shows three impossible figures: the ambihelical hexnut in the lower left-hand corner, tribox in the...
    • twitter:image:src
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_ImpossibleFork.png

  • Link Tags

    4
    • canonical
      https://mathworld.wolfram.com/ImpossibleFork.html
    • preload
      //www.wolframcdn.com/fonts/source-sans-pro/1.0/global.css
    • stylesheet
      /css/styles.css
    • stylesheet
      /common/js/c2c/1.0/WolframC2CGui.css.en

Links

44